
목차
본 포스팅은
'[C#과 유니티로 만드는 MMORPG 게임 개발 시리즈]' 인프런 강의를 수강 후, 개인적으로 배운 내용을 정리합니다.
코드의 경우에는 강사님의 저작권을 훼손할 염려가 있어 결과의 모습, 이론적인 내용을 중점으로 정리합니다.
트리
- 계층적 구조를 갖는 데이터를 표현하기 위한 자료구조
기능이 일부 제한된 그래프이다. 즉, 트리 또한 그래프의 일종.
트리는 순환해서는 안 되며, 한 쪽 방향으로만 쭉 뻗어나아가야 한다. [계층적]구조이기 때문에

트리 관련 용어
- 노드(node): 트리를 구성하는 기본 원소
- 루트 노드(root node/root): 트리에서 부모가 없는 최상위 노드, 트리의 시작점
- 부모 노드(parent node): 루트 노드 방향으로 직접 연결된 노드
- 자식 노드(child node): 루트 노드 반대방향으로 직접 연결된 노드
- 형제 노드(siblings node): 같은 부모 노드를 갖는 노드들
- 리프 노드(leaf (node))/단말 노드(terminal node): 자식이 없는 노드
- 경로(path): 한 노드에서 다른 한 노드에 이르는 길 사이에 있는 노드들의 순서
- 길이(length): 출발 노드에서 도착 노드까지 거치는 노드의 개수
- 깊이(depth): 루트 경로의 길이
- 레벨(level): 루트 노드(level=1)부터 노드까지 연결된 링크 수의 합
- 높이(height): 가장 긴 루트 경로의 길이
- 차수(degree): 각 노드의 자식의 개수
- 트리의 차수(degree of tree): 트리의 최대 차수 = max[deg1, deg2, ..., degn]
- 크기(size): 노드의 개수
- 너비(width): 가장 많은 노드를 갖고 있는 레벨의 크기
[출처 - 나무위키]
트리 같은 경우에는 작년 2학기에 화일처리 수업에서 깨나 고생하면서 익혔던 부분이기때문에 그냥저냥 복습한다는 느낌으로 지나갔다.
AVL트리, B트리 코드를 짜며 죽어나갔던 그 때를 생각하면 트리를 잊을래야 잊을수가 없는것이다...
힙
힙은 완전 이진 트리(노드가 왼쪽부터 채워지는 트리)의 일종으로, 우선순위 큐를 위하여 만들어진 자료구조.
여러 개의 값(노드)들 중에서 우선순위를 갖는 값을 빠르게 찾도록 만들어진 자료구조이다.
기존 이진트리의 경우에는, 부모노드의 왼쪽 자식 노드는 부모노드보다 작으며, 오른쪽 자식 노드는 부모노드보다 컸다.
하지만, 힙의 경우에는 느슨한 반정렬 상태로 단순히 자식노드가 부모노드보다 낮은 우선순위를 갖기만 하면 된다!
이로인해 힙이 기존 이진트리에 비해 갖는 장점이 있다.
기존의 이진트리는 삽입삭제를 하다보면 좌우 밸런스가 무너지는 문제가 발생하고 이를 해결하기 위해서는 AVL 트리라던지, Red-Black 같은 알고리즘을 사용해야 했다.
하지만 힙은 단순히 자식노드가 부모노드보다 낮은 우선순위를 갖도록만 하면 되기 때문에 이러한 문제에서 '비교적' 자유로운 편이다.
- 부모 노드가 가진 우선순위는 자식 노드가 가진 우선순위보다 크다.
- 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있어야 한다.
- 마지막 레벨에 노드가 있을 때는, 항상 왼쪽부터 순서대로 채워야 한다.(완전 이진 트리)
- 노드 개수를 알면, 힙 트리의 구조를 확정할 수 있다.
이러한 힙의 특성으로인하여 힙 트리는 배열을 사용하여 바로 표현 할 수 있다!

힙 트리 삽입[Push]
노드의 개수를 알면, 힙 트리의 구조를 확정할 수 있다고 했다.
그렇기 때문에 위의 힙 트리의 경우에는 9개의 노드를 갖는 힙 트리로 안의 값들이 어떠하든 구조적 모양 자체는 위와 같다. 여기에 하나의 노드가 더 추가되어서 10개라면?

위의 그림과 같을 것이다.
예를 들기 위해 40이라는 Data를 갖는 노드를 추가했다고 하자.
우선 기존 힙 트리의 마지막 자리에 새로운 노드를 추가해 준 후, 그 노드의 부모 노드와 비교를 해 본다.
3과 40, 40이 우선순위 규칙에서 위에 있으므로 두 노드의 데이터값을 교체한다.

그 다음, 또 40과 19의 우선순위를 비교해본다.
마찬가지로 40의 우선순위가 더 위에있으므로 교체
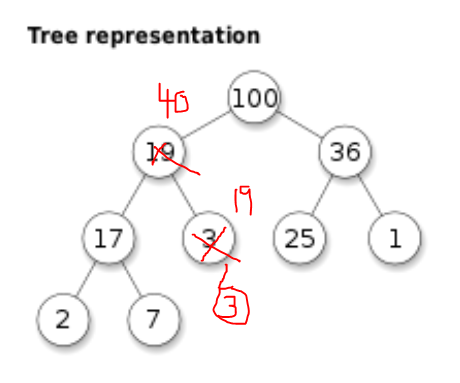
이제는 부모노드가 100으로 자식노드보다 높은 우선순위를 갖게되어 더 이상의 하극상은 발생하지 않는다.
이렇게 되면 삽입이 끝난다.
삽입 후 정렬까지는 최대 Log2n의 복잡도를 갖게 된다.
힙 트리 꺼내기[Pop]
우선순위 큐를 활용했기 때문에 Pop또한 마찬가지로 가장 높은 우선순위를 갖는 값이 나와야 하는데
그 가장 높은 우선순위를 갖는것이 바로 Root Node이다.
Root Node가 무엇인가, 바로 힙 트리의 가장 상위에 위치한 노드이다.
그러므로 바로 그것을 빼 주면...

무슨 히드라도 아니고 머리가 하나 잘렸더니 머리가 두개가 되는 기현상이 발생하고 말아버린다.
힙 구조가 깨져버리고 만 것인데, 그렇게 되지 않기 위해서...
1. 루트 노드를 삭제한다.
2. 제일 마지막(배열로 힙을 구성했을 때 마지막 인덱스를 갖는)노드를 루트노드로 옮겨준다.
3. Push와 마찬가지로 자식노드와 값을 비교하며 차근차근 내려가면 된다.
A* 알고리즘
이제 A*알고리즘을 사용하기 위한 기초지식에 대해서는 다 배웠다.
이제는 A*알고리즘을 사용하여 길찾기를 한다.
사실 미로에서 길 찾는 방법은 크게보면 두 가지 방법이 있다.
- 모든 길을 탐색한 후, 최선의 경로 선택
- 매 선택지에서 최선의 선택
우리가 기존에 했던 길찾기는 1번에 속한다고 보면 된다. 그리고 이 A*알고리즘은 가중치를 사용하여 이 가중치에 따라 좀 더 출구에 가까운 방향을 향해 나아가며 길을 찾는다고 보면 된다.
그리고 이 과정에서 크게 다익스트라와 우선순위 큐(힙)을 사용하게 된다.
지금까지 가장 최소의 비용으로 도달한 지점부터 탐색하는 다익스트라 알고리즘의 원리를 차용한 것으로, A* 알고리즘은 현재 상태의 비용을 g(x), 현재 상태에서 다음 상태로 이동할 때의 휴리스틱 함수를 h(x)라고 할 때, 둘을 더한 f(x) = g(x) + h(x)가 최소가 되는 지점을 우선적으로 탐색하는 방법이다. 이 f(x)가 작은 값부터 탐색하는 특성상 우선순위 큐가 사용된다. 휴리스틱 함수 h(x)에 따라 성능이 극명하게 갈리며, f(x) = g(x)일 때는 다익스트라 알고리즘과 동일하다.
https://namu.wiki/w/A*%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
A* 알고리즘 - 나무위키
이 저작물은 CC BY-NC-SA 2.0 KR에 따라 이용할 수 있습니다. (단, 라이선스가 명시된 일부 문서 및 삽화 제외) 기여하신 문서의 저작권은 각 기여자에게 있으며, 각 기여자는 기여하신 부분의 저작권
namu.wiki

A* 알고리즘을 사용하여 만든 길찾기
현재 A*알고리즘에 대한 설명이 상당히 미진하다.
강의에 따라 코드를 따라쳐보고, 어느정도는 이해했지만 완전히 내 것으로 습득했다는 수준은 못된다.
추후 진도가 더 나아감에 따라 새로 적용할 부분이 생긴다면 강의의 도움없이 코드를 작성하여 내 것으로 만든 후 설명을 다시 작성해보고자 한다.
'Unity3D > 유니티 공부' 카테고리의 다른 글
| [Unity2D 공부] 기초적인 클리커 게임 제작 (0) | 2021.06.09 |
|---|---|
| [Unity2D 공부] 이동과 충돌 학습정리 (0) | 2021.06.07 |
| [Unity 게임 개발을 위한 C# 공부 일지] 길찾기 - 2 (그래프) (0) | 2021.05.12 |
| [Unity 게임 개발을 위한 C# 공부 일지] 길찾기 - 1(미로 생성, 우수법) (0) | 2021.05.10 |
| [Unity 게임 개발을 위한 C# 공부 일지] TextRPG 기초 제작 - 전투 (0) | 2021.04.07 |